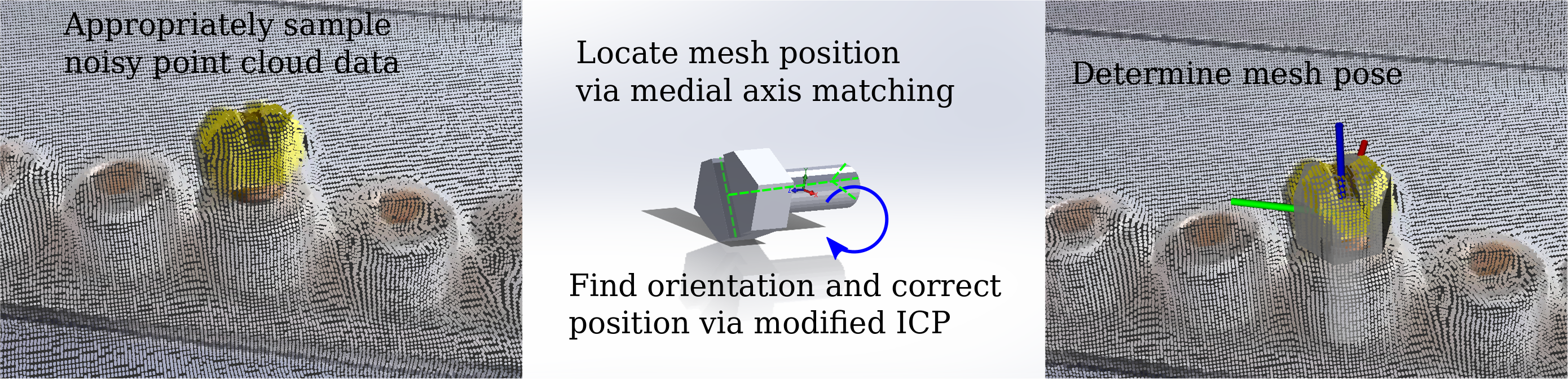
Overview

We present an implementation of our medial-axis and face-based 3D Pose Recognition Algorithm. This algorithm takes a library of meshes and fits the poses in a provided single point cloud. Our implementation is meant to be used as part of an interactive robot authoring program for manufacturing, meaning there is an emphasis on both performance and reliability.

implementation teaser

Figure 1: Teaser of FAMrec Results

Motivation

There are many industries where 3D recognition of objects can be useful. For example, autonomous driving can benefit from being able to quickly recognize and localize objects in the environment. We desire a reliable 3D Object pose recognition for aviation manufacturing, where robotics can be used to manipulate recognized objects to complete tasks. These environments are semi-structured, meaning the objects (e.g., bolts, screws, tools) are often known ahead of time, but the precise locations may not be known, warranting classification and pose recognition. Notably, as much of the development involves composites and lightweight metals, there is little color differentiation in the environment.

target setup

Figure 2: Target setup of algorithm

When originally searching for a method for our application, we were unable to find a reliable method that could identify objects in our prototype environment, which inspired us to try to create a method. More detail is available in our original proposal.

Estimating object and pose recognition from a point cloud is an area of large recent interest. We provide a partial review of relevant, recent work to appropriately contextualize the key ideas of our method. Given that point clouds often contain large amounts of noise, it is common to use robust fitting methods in determining scene geometry. Many methods (e.g., [1][2]) use a modified version of RANSAC, where primitive geometry is estimated based on evaluating random minimal sets of points against continuous surfaces (e.g., planes, spheres, cones, etc). In a few methods, the general RANSAC method is extended to arbitrary mesh geometry. For example, Papazov et al. [3] developed a method which sample an arbitrary mesh as a point cloud and uses two-point geometric correspondences to determine where a mesh is located in the scene. Other recent methods use neural network approaches to fit an arbitrary mesh. Methods commonly use a convolutional neural network (CNN) approach. For example, PointNet++ [4] can identify objects in an scene by first segmenting the scene and then classifying each of the segments through a hierarchical network struture. In contrast to the manufacturing environment described above, neural network approaches are often employed to allow for variance in the specification of objects.

Approach

Existing approaches to arbitrary mesh recognition often use either a neural-net or RANSAC-based kernel. In our work, we have developed a method that uses the medial axis of the mesh to determine hypothesis mesh keypoints and a modified version of Iterative-closest point (ICP) to determine a more precise mesh pose. In our approach, we tried to use geometric features wherever possible.

In developing this approach, we built multiple other implementations. First, we developed an Efficient RANSAC [1] program that could identify spheres and cylinders. We then created our first algorithm Face-Based-Features RANSAC (FBF ransac) which was a RANSAC-based kernel that used face to point correspondence instead of point to point typical of other RANSAC methods. Both of these implementations are also in github, but are not discussed further. More detail on these can be found in our midterm report.

Implementation (FAMrec)

Required Packages

We provide a full package python package for our implementation. This was tested using python 3.6. One of our goals was to create as compact and simple of code as possible to promote longevity. Our code is not yet optimized for performance.

Required Packages: numpy, trimesh, point_cloud_utils, pykdtree, pyntcloud, gimpact, progress, open3d

Suggested package install directions (including some packages for FBF-RANSAC):

pip3 install numpy
pip3 install rtree
sudo apt-get install libspatialindex-dev
pip3 install trimesh
pip3 install git+git://github.com/fwilliams/point-cloud-utils
pip3 install pykdtree
pip3 install pyntcloud
pip3 install progress
pop3 install gimpact
pip3 install open3d
or conda install -c conda-forge point_cloud_utils

Data Structure

For FAMrec there are a few main classes that build up the method:

Additionally, the EfficientRANSAC and FBFRansac folders have their own classes and scripts found in separate folders. There is also a utilities folder that provides several scripts for converting file formats, etc.

Core Algorithm

Medial Axis Matching

One of the simplest ways to differentiate two objects is their scale. If you can determine the scale of the geometry in the scene, many objects can be quickly ruled out. One way of getting at this idea of localized scale is through the medial axis of the scene. The medial axis is defined as the set of all points that have two or more equidistant scene points. By searching for points on the medial axis of the scene that have the right distance-to-scene value, it is possible to search for locations with an appropriate scale.

Medial Axis

Figure 3: Left) Example of Medial Axis adapted from [5] Right) Discretized medial axis representation of a toy screw

At the core of this algorithm is the ability to find medial axis points that have approximately the radius we are looking for. While there are a number of algorithms to find medial axis points from a geometry, they are generally highly sensitive to noise in the cloud. The need to robustly identify a single point on the medial axis that is a certain distance from the scene motivates the following, Mean Shift inspired, novel algorithm:

PROGRAM FindMedialAxisPoint:
  # Description: Attempts once to find a medial axis 
    point in the scene with a given radius. 
  # Inputs: 
    PointCloud  - The set of 3d points representing the scene
    Radius      - The target radius
    dr          - Noise tolerance
  # Outputs: Position or None
  Position <= Random-Point-Near-Cloud
  
  WHILE iterations < MAX_ITERATIONS 
        && PositionDelta > EPSILON:
    neighbors <= Points-within-(Radius + 2dr)-of-Position
    
    IF WeightedAverage(DistanceTo(neighbors)) ~= Radius
      EXIT
    END
    idealPositions <= Points-(1*Radius)-Away-from-neighbors
    Position <= WeightedAverage(idealPositions)
  END
  
  Position <= None
END

Here we use a modified Woods-Saxon distribution as a weighting function to compute the weighted average.

This ensures that points inside of the target radius are always considered heavily, while maintaining a smooth transition from “relevant points” to “irrelevant points” as they get farther away, which allows for consistent convergence.

Now that we have an algorithm for finding locations of similar geometric scale, we need to profile each object in our database to determine what we are looking for and how that relates to the object. This is done by simply sweeping out a range of radii of appropriate scale (as determined by the size of the bounding box) and looking for medial axis points at that scale. When profiling an object, we use a thickness (dr) equal to 2% of the target radius.

Once we have generated profiles for our objects and cached them on disk, we are ready to look for the objects in a scene. This is approached straightforwardly by looking for each possible object in the scene in turn. For each object, a keypoint is randomly selected, and the same algorithm used to profile the object is used to find a keypoint with that radius in the scene. If one is found, then modified ICP is used to align the object.

Modified Iterative-Closest Point

When determining the pose of 3D objects from noisy data, it is common to use an Iterative-closest point algorithm as a means of refining an initial estimate of the object pose. We extend the core algorithm in two key ways to make it amenable to our object recognition formulation.

As a brief reminder, the premise of ICP is to complete an optimal rotation and translation in order to align two sets of points. The sets of points are constructed by finding the closest corresponding points between the sets. The optimal translation and rotation can be solved as a linear system using SVD.

First, we define a custom weighting function cognizant of our face-matching based approach to recognition. The core ICP algorithm is designed to compute the optimal rotation and translation to align two sets of points. Often, these will be simliar types of data (e.g., points from a point cloud and points sampled on a mesh). In our algorithm, we compare the center points of the mesh faces to the points on the point cloud. Naturally, this prescribes some error for the matching related to the size of the faces. In order to combat this, we implement a weighting function that punishes large mesh faces in the fitting. Our weighting function also considers distance between the matching points as is a common choice in weighting functions. Our final weighting functions combines these two ideas and can be computed as:

where is the distance between the face and the closest point in the point cloud, is the maximum distance considered in the ICP algorithm, is the area of the mesh face, and is the largest face in the mesh.

Second, we implement a random restarts framework around the ICP algorithm. The medial axis reliably gives candidate positions for the mesh, but not rotation. In order to prevent the ICP from getting caught in local minima during iterations, we use a random restarts approach where each restart is given a random orientation (drawn from the Haar distribution for SO(3)). In our implementation, we use 10 random restarts. Most our geometry had a single principal axis, and thus escaping local minima simply required one rotation that avoided the “upside down” configuration. More complicated geometry subject to additional minima might require more restarts.

Finally, to provide a level of robustness to occlusion that is common particularly when point clouds are constructed from a single image, we implement the occlusion method described in [6] . During each ICP iteration only a percentage of the closest corresponding face-point combinations are selected. From experimental tuning, we choose to use 80 percent of the faces, which allows for some occlusion-handling while not skewing results for non-occluded objects.

Pose Validation

Once the algorithm comes up with a potential pose, it must be validated against the scene. This is done by comparing a threshold hold value to a Hausdorff-inspired mesh-to-scene distance metric.

Where here, is the closest scene point to face , which has normal . This metric is compared against the expected error in scene point measurement. If the model fits perfectly, we would expect each of the faces to have corresponding scene points lying on the face (within error tolerance). If the model is incorrectly oriented, or if it is simply the wrong model, we would expect at least one face to be significantly displaced from the scene.

Results

General results

We chose to evaluate our method by testing it on a new set of meshes. We use the freely available Toy Toolkit from free3D. This set is comprised of seven meshes: hammer, pliers, saw, screw, screwdriver, spanning wrench, and wrench.

We created 3 random scenes that contain all seven objects with randomized poses. Each example scene is a point cloud consisting of 100,000 points. We perform a combinatorial (e.g., 7 choose 3) analysis for each of the scenes and report the confusion matrix results. We added an additional category to the standard confusion matrix for ‘Misfit True Positive’ which is when the correct model is selected, but the pose is incorrect (more common of competing methods). The results are reported in Table 1. Note: While the results may seem to be a low percentage, it is on part with existing methods (e.g., ObjRecRANSAC). More detail and comparison is found below.

Object True Positive Misfit True Positive False Negative True Negative False Positive
Hammer 24 0 19 53 9
Pliers 10 0 26 45 28
Saw 13 1 24 51 16
Screw 7 5 30 60 0
Screwdriver 10 1 32 58 4
Spanning Wrench 10 0 27 49 19
Wrench 4 3 19 23 83
Table 1: FAMrec Combinatorial Testing Results

We find that our system is able to recognize objects across a variety of shapes and sizes, though we still believe the algorithm can be improved as far as reliability. In particular, our method had a challenge with the wrench model which was often mistaken as a series of screws. Such a classification is still a potential issue with our formulation where smaller geometry with similar local scales can be found within larger geometry. As partial future mitigation, we propose to cull the scene space as objects are found and do mesh identification ordered by decreasing volume. More details are below. For recognition of the wrench (and other objects), the low true positive rates suggest we should further refine our correspondence criteria to more reliably get matches.

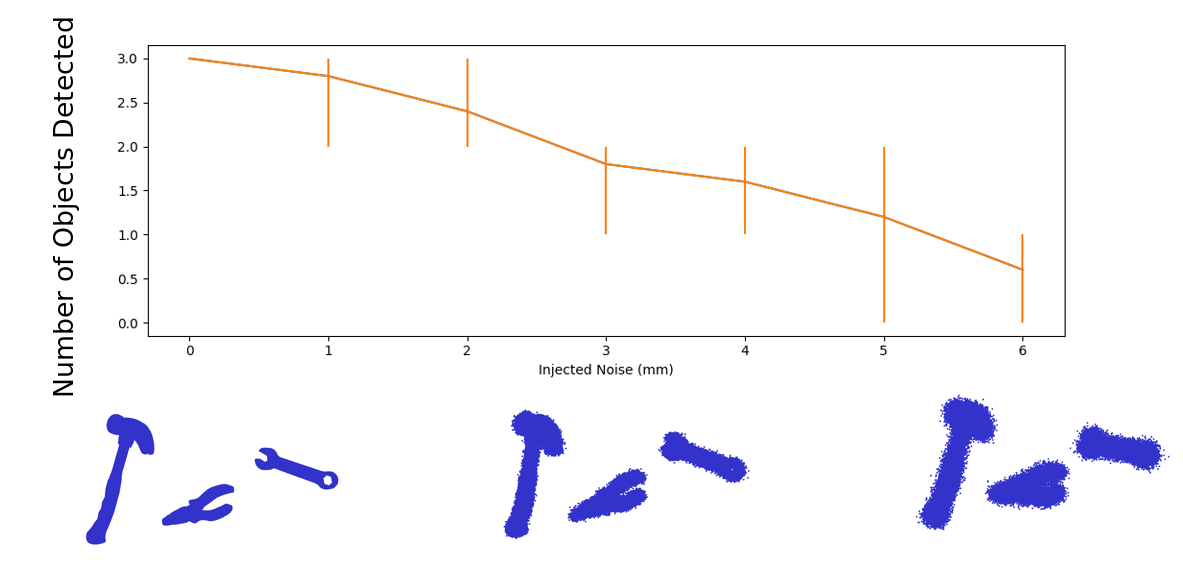
Recognition with Point Cloud Noise

We desire to use our algorithm with point clouds from real 3D scenes, which requires some level of robustness to measurement noise. To test our algorithm, we create a 3 object recognition scene and perform 5 recognition trials at various levels of injected Gaussian noise. As seen in the figure below, our algorithm performs well for less than 2 mm of injected noise. This is comparable to the expected noise measured from our actual camera.

noise testing

Figure 4: Noise Testing

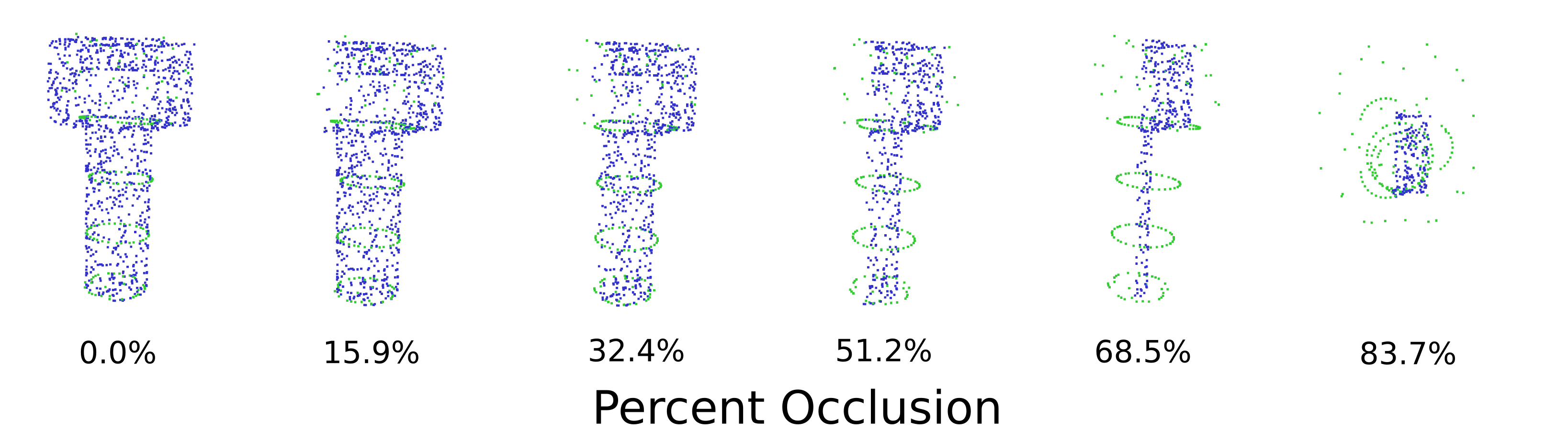
Recognition under Occlusion

The medial-axis part of our algorithm can still identify geometry under large percentages of occlusion, provided that convex sections of the mesh are still visible. To test our ICP algorithm against occlusions, we artificially remove sections of a screw model and use ICP to recognize the pose. As a reminder, our algorithm is designed to still function seamlessly for less than 20 percent occlusion. In testing, we have found that our algorithm is robust to small amounts of occlusions (<30%). Below, we show one example of occlusion testing against a model of a screw. In this figure, blue points are the point cloud points used for fitting and the green points are an outline of the fit mesh. At around 50 percent occlusion, the mesh fit starts to have notable error. At this point, the principal axis of the remaining points of the screw starts to align with the mesh principal axis. This is expected behavior for an ICP-type algorithm. At approximately 80 percent, the mesh fit is incorrect. More discussion about occlusions can be found below in the future work.

occlusion testing

Figure 5: ICP Occlusion testing for the Toy Screw model from the side angle

Issues/Limitations

The primary limitation to this algorithm is that its runtime is underwhelming compared to other solutions with a highly refined implementation. In the worst case of isolated object classification (a task which this was not designed for), it can take upwards of 2 minutes to perform a single classification. While there is still signficant room for improvement in the runtime of this implementation, the complexity of improving it has thus far been cost prohibitive.

Unfortunately, due to building access issues, we were unable to test our algorithm against real objects from the robot Kinect camera. In the future, we hope to do further testing and iteration to make our algorithm work with the actual robot system.

Comparisons

We compare our method with our implementation of Efficient RANSAC as well as with two state of the art open-source algorithms: ObjRecRansac and PointNet++. Details of the implementations and the comparisons follow:

Efficient RANSAC

As a first basic test, we compare FAMrec to our Efficient RANSAC implementation for recognizing sphere and cylinder primitives. Our goal here is only to perform a basic validation test of our method. For these two particular primitives they are well suited for FAMrec as the medial axis for the sphere is a single point and for the cylinder, it is a straight line. We construct a test scene with two of each object. While efficient RANSAC can find any sphere or cylinder, FAMrec is based on mesh recognition and is therefore not scale and parameter invariant. Thus, both of the spheres and cylinders are the same size as the corresponding meshes. Efficient RANSAC Comparison

Figure 6: Efficient RANSAC Comparison

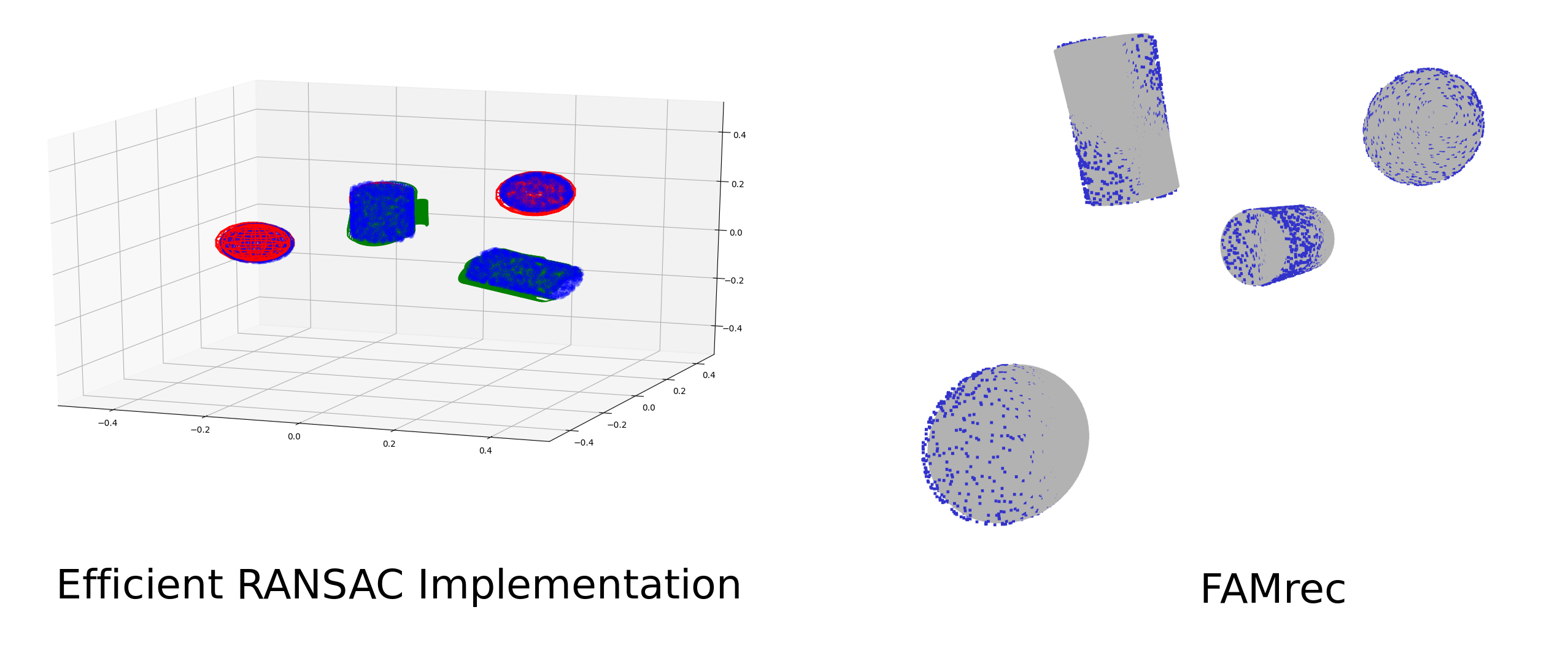
Both of our algorithms are able to find and determine the pose of the spheres and cylinders. We ran each approximately 10 times and both algorithms find all four objects in the majority. As seen in the figure, Efficient RANSAC occasionally has false positives. FAMrec reliability gets the objects, but occasionally will not yield a perfect fit as a result of the ICP occlusion algorithm (not pictured).

ObjRecRANSAC

Example ObjRecRANSAC

Figure 7: Example of ObjRecRANSAC Results

ObjRecRANSAC is a RANSAC-kernel based method that uses random sampling to identify geometry in the environment. The original algorithm was proposed by Papazov et al. [3] in 2011. The key idea is to identify key sets of points that can be used for recognition as part of a RANSAC algorithm.

Note: The implementation used for the comparison can be found here. In order to build, we found that a very specific set of libraries was needed. This implementation is built against PCL and VTK. In order to get it to work, we choose to manually build VTK 5.10 from source and then to manually build PCL 1.8.0 from source against this VTK. Having other system versions of VTK seems to cause intermittent seg faults as there are many levels in which VTK is included as a library and it is difficult to change the CMake to force a particular version.

Both ObjRecRANSAC and our method take a set of meshes (e.g., stl) and find instances in a provided 3D point cloud. As such, it was relatively straight forward to run a comparison. We created 3 example scenes to test the algorithms. We run the same combinatorial analysis as was run on FAMrec.

Object True Positive Misfit True Positive False Negative True Negative False Positive
Hammer 13 21 5 6 61
Pliers 38 0 0 10 57
Saw 16 27 2 10 50
Screw 0 0 45 60 0
Screwdriver 4 0 28 35 41
Spanning Wrench 0 0 28 31 46
Wrench 4 29 9 14 49
Table 2: ObjRecRANSAC Combinatorial Testing Results

We find that FAMrec has a slightly higher true positive rate in recognition. FAMrec also has significantly fewer false positives. ObjRecRANSAC is highly dependent on a radius search term to make the RANSAC process tractable. We attempted to tune ObjRecRANSAC to give the most favorable results, but ultimately the search radius makes it not particularly amenable to objects of various scales. This is why the screw is never found. Attempts to make the radius smaller made the program unable to recognize any of the meshes. ObjRecRANSAC had a consider number of misfit true positives, which we define as when the correct mesh is selected, but it is not fit correctly. These are not reported as true positives in the below confusion matrix. Interestingly, while this type of behavior might make sense for FAMrec where the ICP may be caught in a local minima, it goes a bit against the theory used in ObjRecRANSAC. ObjRecRANSAC attempts to find point-to-point and normal-to-normal correspondences, so in theory, the pose should also be recovered. As we saw in practice with Efficient RANSAC, however, these normals are constructed via nearest neighbors and often do not provide robust normal estimations which can greatly impact the theory.

Confusion Results

Figure 8: Confusion Results

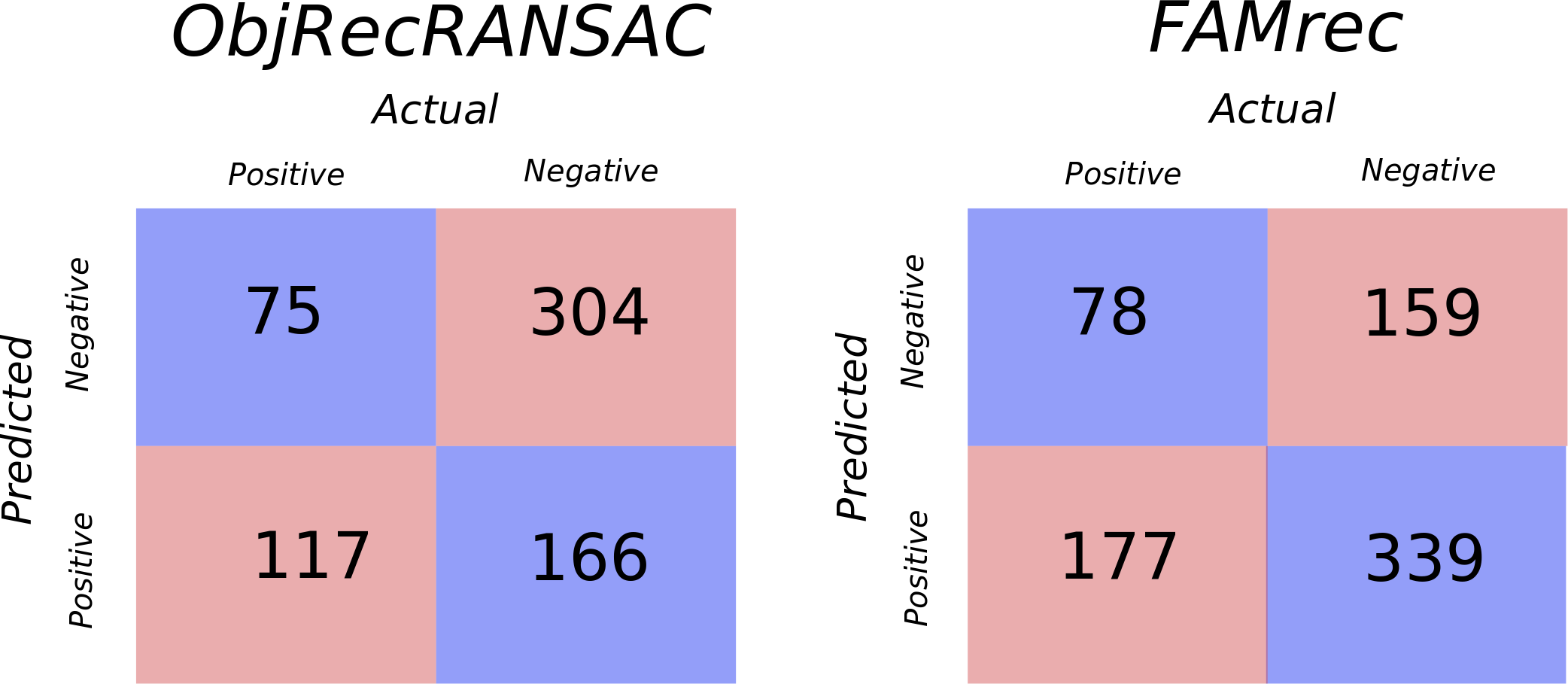
While our algorithm only performs marginally better than the current state of the art, we believe with future work, we can greatly improve our algorithm. See the ‘future work’ section below.

PointNet++

PointNet++ is a state of the art neural-network based approach for object recognition. The algorithm was proposed in Qi et al. [4] in 2017. Using a variety of custom pre-processing layers and tensorflow, this approach is trained to recognize objects and their specific classification.

Note: The implementation used for the comparison can be found here. This implementation requires Tensorflow and NVIDIA CUDA Drivers. We were able to build the package using CUDA 9.0 and TensorFlow something. As a neural-net approach, the system required training. We trained using the ModelNet40. Note: we trained using a single 4 GB GPU over the course of approximately 20 hours. Due to memory restrictions, the training was ran with a sub-recommended batch size, which may partially explain the lower classification results below.

pointnet example objects

Figure 8: PointNet++ Example Objects

PointNet++ is designed as a classifier, meaning for an input point cloud of a single object, it will return a classification from the labels used during training. Thus, a direct comparison similar to above is not possible. Instead, we focus on a comparison where we use FAMrec as a classifier for a randomly-selected set of objects from the same classes that the PointNet++ model was built upon. We train PointNet++ using the ModelNet40 database from Princeton [7] (link). From the test set of ModelNet40, we extract 30 randomly sampled meshes (We were unable to convert 10 of the classes to a format that works with our mesh importing system). For each of these 30 objects, we load them 5 times with random orientations in PointNet++ and get the classification. We also load them 5 times with random orientations into FAMrec and get what object is recognized (Note: FAMrec might return no object or possibly multiple - it is not a classifier). This gives us a biased, but reasonable metric to compare the methods. The following two tables have the classification results:

PointNet++
Object Classification Object Classification Object Classification
bed 0.0 door 0.0 radio 0.4
bench 0.4 flower pot 0.0 range hood 0.0
bookshelf 0.0 glass box 0.0 sink 0.0
bottle 0.0 keyboard 0.2 stairs 0.4
bowl 0.2 lamp 0.4 stool 0.0
car 0.6 laptop 0.0 tent 0.2
chair 0.2 mantel 0.2 toilet 0.0
cone 0.4 person 0.0 tv stand 0.0
cup 0.0 piano 0.0 vase 0.6
curtain 0.4 plant 1.0 wardrobe 0.0
Table 3: PointNet++ Classification Testing
FAMrec
Object Classification Object Classification Object Classification
bed 0.0 door 0.0 radio 0.0
bench 0.4 flower pot 1.0 range hood 0.0
bookshelf 0.8 glass box 0.6 sink 0.8
bottle 0.2 keyboard 0.0 stairs 0.0
bowl 0.4 lamp 0.0 stool 0.4
car 0.2 laptop 0.0 tent 0.0
chair 0.0 mantel 0.0 toilet 0.0
cone 0.0 person 1.0 tv stand 0.0
cup 1.0 piano 0.2 vase 0.8
curtain 0.4 plant 0.6 wardrobe 0.0
Table 4: FAMrec Classification Testing

Overall, the accuracy of our method (30%) compares favorably to that of PointNet++ (18.7%). However, the following caveats should be considered:

  1. PointNet++ performed significantly worse on our selection of individual objects than the reported dataset average.
  2. With the current implementation of our algorithm, it takes much longer to reach a conclusion than PointNet++.
  3. Some of the models, like the car, contain interior detail. This is an unrealistic piece of information that causes our algorithm to behave erratically (i.e. finding the car, but also attempting to identify objects inside of the car).
  4. The scale of the models are inconsistent. While this shouldn’t affect fundamental classification results, it results in unexpected confusion, like mistaking a bed for a car, that our algorithm should be robust to in real applications.

Conclusions and Future Work

The results suggest that this algorithm is, in many ways, on par with others in the field. It shows the potential to beat other competing algorithms, and even compare favorably against modern neural network approaches if this were refined significantly. However, currently this implementation is still in its technical infancy. There are a number of improvements that could be made to improve the practicality, and accuracy. The most signficant of which is the concept of “culling space” as we look for objects. Currently, if we fail to find a keypoint at a certain radius, we don’t gain any information and might sample the same region at the same radius again. This is highly problematic when the target object represents a very small portion of the scene. If a region could be determined to not contain an object, the convergence of the algorithm would be sped up dramatically.

Secondly, this algorithm was designed with a highly parallel hardware platform in mind. The search for keypoints is simple and can be completely parallelized to take advantage of modern GPUs. We expect that this would, again, dramatically improve the performance of this algorithm.

Thirdly, if the object database is very large and the odds of any one object being in the scene are low, the algorithm performs very poorly. In that case, it would be much more efficient to look for keypoints in the scene and then match them to objects in the database. Going in this direction would likely require significant modifications to the core algorithm.

Lastly, there is room for improvement around robustness to occlusions. In real scenes, it is unlikely that we will have a full 360 degree view of the object. Most commonly we will have a single perspective, which would be similar to 50% occlusion. There are directions that can be taken to improve this, but in general this is an active area of research, as there is no broadly applicable solution. In addition to making our algorithm more robust to occlusions, we also might experiment with recognizing occlusions. With our prototype setup in which a camera is mounted to a robot, knowing an occlusion is occurring may inform the robot to change its pose to give the camera a less occluded view.

References

[1] Ruwen Schnabel, Roland Wahl, and Reinhard Klein. Efficient ransac for point-cloud shape detection.Comput. Graph. Forum, 26:214–226, 06 2007. doi: 10.1111/j.1467-8659.2007.01016.x.
[2] Liangliang Nan and Peter Wonka. Polyfit: Polygonal surface reconstruction from point clouds. 07 2017.doi: 10.1109/ICCV.2017.258. [3] Chavdar Papazov, Sami Haddadin, Sven Parusel, Kai Krieger, and Darius Burschka.Rigid3d geometry matching for grasping of known objects in cluttered scenes.The InternationalJournal of Robotics Research, 31(4):538–553, 2012.doi:10.1177/0278364911436019.URLhttps://doi.org/10.1177/0278364911436019.
[4] Charles R. Qi, Li Yi, Hao Su, and Leonidas J. Guibas. Pointnet++: Deep hierarchical feature learning onpoint sets in a metric space. InProceedings of the 31st International Conference on Neural InformationProcessing Systems, NIPS’17, page 5105–5114, Red Hook, NY, USA, 2017. Curran Associates Inc. ISBN9781510860964 [5] Demirci M.F. Boluk, A. Object recognition based on critical nodes.Pattern Anal Applic, 22:147–163,2019. doi: 10.1007/s10044-018-00777-w.
[6] P. Liu, Y. Wang, D. Huang and Z. Zhang, “Recognizing Occluded 3D Faces Using an Efficient ICP Variant,” 2012 IEEE International Conference on Multimedia and Expo, Melbourne, VIC, 2012, pp. 350-355.
[7] Z. Wu, S. Song, A. Khosla, F. Yu, L. Zhang, X. Tang and J. Xiao. 3D ShapeNets: A Deep Representation for Volumetric Shapes. Proceedings of 28th IEEE Conference on Computer Vision and Pattern Recognition (CVPR2015)